Imaginary numbers
Published:
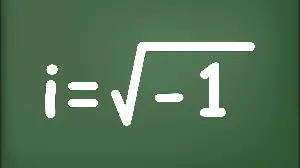The idea of “imaginary” or “unreal” numbers first arose when mathematicians encountered equations that had no solutions in the real number system. For example, the equation x^2 + 1 = 0 has no solutions in the real numbers, since the square of any real number is non-negative. However, it was noticed that if we introduce a new number, denoted by the symbol “i”, such that i^2 = -1, then the equation x^2 + 1 = 0 has two solutions, namely x = i and x = -i.
The concept of imaginary numbers was initially met with skepticism and resistance by some mathematicians, who regarded them as a mathematical curiosity or even as absurd. For example, the mathematician and philosopher René Descartes expressed doubt about the reality of imaginary numbers, stating that “I do not conceive how there can be a quantity that is the square of minus one.”
However, other mathematicians recognized the usefulness of complex numbers and developed techniques for working with them. The Swiss mathematician Leonhard Euler was particularly influential in developing the theory of complex numbers and using them to solve mathematical problems. In particular, he developed the formula e^(ix) = cos(x) + i sin(x), known as Euler’s formula, which relates complex numbers to trigonometry.
The development of complex numbers was furthered in the 19th century by mathematicians such as Carl Friedrich Gauss, William Hamilton, and Augustin-Louis Cauchy, who extended the theory of complex numbers to include the idea of “analytic functions,” which are functions that can be expressed as a power series in the complex variable.
Today, complex numbers are a fundamental part of mathematics and are used in many different areas of science and engineering. They are used to represent phenomena that have both real and imaginary components, such as electrical circuits and quantum mechanics. Complex analysis, the study of functions of a complex variable, is an important branch of mathematics that has many applications in physics, engineering, and other fields.
In conclusion, the invention and development of imaginary numbers are a testament to the power of human creativity and ingenuity. What started as a mathematical curiosity has become an essential part of modern mathematics and science. The history of imaginary numbers is a reminder that seemingly impossible problems can often be solved with a little creativity and a willingness to think outside the box.
In the realm of philosophy, there are certain thought experiments that challenge the way we think about the nature of identity, change, and continuity. One such thought experiment is the paradox of Theseus’s Ship, an ancient puzzle that has intrigued philosophers for centuries. At its core, it raises profound questions about what it means for something—or someone—to remain the same over time, even when it undergoes significant changes. 
In life, we all face challenges. Whether at work, in relationships, or in the pursuit of personal goals, problems are an unavoidable part of the journey. These obstacles can test our patience, resilience, and growth. However, some people seem to create their own problems—sometimes without even realizing it. They may subconsciously make choices that lead to unnecessary difficulties or adopt a mindset that attracts more conflict. Then, they take on the role of the victim, acting as though life has been unfair to them. This behavior not only creates emotional strain for those around them but is also deeply harmful to the person doing it. Why? Because those who play the victim of their own problems always lose. They lose control over their lives, their potential for growth, and their ability to change their circumstances. 
The saying “If you’ve become arrogant, you no longer need another enemy.” carries profound wisdom about the dangers of arrogance and how it can become a person’s greatest adversary. Arrogance blinds us to our own flaws, prevents us from learning from others, and often isolates us from those who could help us grow. When we allow arrogance to take hold, we sabotage our own success, relationships, and personal growth, making external enemies unnecessary—our worst enemy becomes ourselves. We become so consumed with self-importance that we fail to recognize the opportunities for improvement and connection all around us.