Embracing the Significance of Every Moment
Published:
In the vast expanse of time, the reality echoes—no matter who we are or what we do, the memory of our existence fades with the passing years. This is an intrinsic part of the human experience, prompting reflections on the transient nature of legacy and the imperative to cherish every moment we have. Yet, even as our names may be forgotten, the ripples of our actions, kindness, and love can subtly shape the lives of others, weaving us into the endless fabric of humanity’s story. Read more
The Unexpected Hanging Paradox is a fascinating thought experiment that has puzzled many great minds in the fields of philosophy, mathematics, and logic. The paradox was first introduced by Raymond Smullyan in 1979 and has since captured the attention of many curious minds. This paradox raises many interesting questions about logic and reasoning, and it’s a great example of how philosophy can challenge our assumptions and push us to think in new ways. 
Zeno’s Paradox is a classic thought experiment in mathematics and philosophy that challenges our understanding of infinity, motion, and the nature of reality. The paradox was first proposed by the ancient Greek philosopher Zeno of Elea in the 5th century BCE, and it has since been the subject of much debate and discussion in the fields of mathematics and philosophy. Through examples such as Achilles and the Tortoise or the Dichotomy Paradox, Zeno illustrated how infinite divisions of space and time can seemingly make motion impossible, sparking profound inquiries into the nature of continuity and change. 
Berry’s Paradox is a curious and thought-provoking paradox in mathematics and philosophy that challenges our understanding of truth, reference, and meaning. The paradox was first proposed by Bertrand Russell’s student G. G. Berry in the early 20th century, and it has important implications for our understanding of language, semantics, and the nature of mathematical reasoning. The paradox has significant implications for the philosophy of language and mathematics, and it continues to be a topic of interest for scholars and educators. 
Hilbert’s Paradox is a thought experiment in mathematics which was first proposed by the renowned mathematician David Hilbert in the early 20th century. The paradox challenges our intuition and understanding of the concept of infinity. It has important implications for our understanding of the nature of mathematical objects and the limits of human knowledge. Hilbert’s Paradox is a prime example of a problem that highlights the counterintuitive nature of infinity and the challenges that arise when dealing with infinite sets. By illustrating how an infinite hotel can always accommodate more guests, even when fully occupied, it demonstrates the strange and paradoxical properties of infinite systems. 
The Birthday Paradox is a fascinating concept in probability theory that may seem counterintuitive at first. The paradox arises from the fact that the probability of two people in a room sharing the same birthday increases much more rapidly than one might expect as the number of people in the room grows. This phenomenon can be explained by the fact that there are many more possible pairs of people as the number of people in the room increases. The Birthday Paradox has important implications for many fields, including cryptography, where it is used to calculate the probability of a collision between two hash values. 
The Banach-Tarski Paradox is an incredible theorem in mathematics discovered by Stefan Banach and Alfred Tarski in the 1920s. The paradox challenges our intuition about the nature of space and the way we measure geometric objects. The paradox has major implications for several areas of mathematics and the philosophy of science, including the concept of infinity, set theory, and the foundations of mathematics itself. Its unexpected findings have fascinated mathematicians and philosophers for almost a century, and the Banach-Tarski Paradox remains one of the most intriguing and intensely studied topics in the field of mathematics to this day. 
The Liar Paradox is a classic paradox in logic and philosophy that has perplexed scholars for centuries. The paradox arises from a self-referential statement that leads to a contradiction, challenging our assumptions about truth and meaning. Numerous solutions have been proposed, but the paradox continues to spark debates and discussions among scholars, making it an essential topic for anyone interested in the foundations of logic and the nature of truth. 
The Barber Paradox is a classic example of a self-referential paradox, which was first introduced by the British logician Bertrand Russell in 1901. The Barber Paradox involves a barber who shaves all men who do not shave themselves. This paradox is self-contradictory and challenges our understanding of language and meaning. The Barber Paradox has been a subject of much discussion and debate among philosophers and logicians, and it has contributed significantly to the development of the foundations of mathematics and the philosophy of language. 
Russell’s Paradox is one of the most notable paradoxes in mathematics and logic. It was first identified by Bertrand Russell, an English philosopher and logician, in 1901. The paradox arises when considering the set of all sets that do not contain themselves as members. The paradox is considered a significant challenge for many modern approaches to set theory, and has contributed significantly to the development of the philosophy of language, logic and mathematics.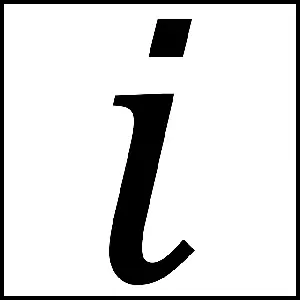 
Mathematics began as a way to quantify our world, to measure land, predict the motions of planets, and keep track of commerce. But there was a problem that was considered impossible to solve. The secret to solving it was to separate math from the real world, to split algebra from geometry, and to invent new numbers so fanciful they are called imaginary. In this post, we will explore how imaginary numbers were invented and their relevance today. 
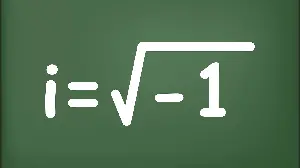The idea of “imaginary” or “unreal” numbers first arose when mathematicians encountered equations that had no solutions in the real number system. For example, the equation x^2 + 1 = 0 has no solutions in the real numbers, since the square of any real number is non-negative. However, it was noticed that if we introduce a new number, denoted by the symbol “i”, such that i^2 = -1, then the equation x^2 + 1 = 0 has two solutions, namely x = i and x = -i.